Mục lục

Bài 1: Phương pháp đánh giá dịch bệnh, từ đó đưa ra các quyết định trong phòng chống dịch bệnh [được chuyển đến đây từ link gốc đã xuất bản ngày 10/7/2021]

Bài 2: Một phương pháp dự báo dịch bệnh

Bài 3: Sóng Siêu lây nhiễm

Bài 4: Bàn thêm về mô hình: khoảng thời gian nối tiếp và số ca được báo cáo

Bài 5: Một góc nhìn định lượng cho vắc-xin

             Bài 5a: Phụ lục - Lựa chọn khoảng thời gian giữa hai mũi vắc-xin

Bài 6: Một giải pháp

Phụ lục: Các bài phân tích làn sóng dịch Covid-19 thứ 4 từ 14/07 - 29/08

Phương pháp đánh giá dịch bệnh, từ đó đưa ra các quyết định trong phòng chống dịch bệnh

1. Hệ số lây nhiễm cơ bản (basic reproduction number) và khoảng thời gian nối tiếp (serial interval)

Đối với một bệnh dịch, hệ số lây nhiễm cơ bản R₀ và khoảng thời gian nối tiếp trung bình T là hai tham số quan trọng nhất. Ta bắt đầu bằng một ví dụ trong kinh tế. Để đánh giá tăng trưởng kinh tế, ta tính GDP và nó được tính cho quãng thời gian một năm. Đối với một bệnh dịch, tương tự ta cần tính hai tham số R₀ và T (đơn vị của T là ngày).

Trong giai đoạn đầu của bệnh dịch, trung bình 1 cá thể bệnh sẽ sinh ra R₀ cá thể bệnh mới trong khoảng thời gian T. Từ đó ta có thể tính ra rằng, trong giai đoạn đầu n*T ngày, nếu R₀ > 1, trung bình 1 cá thể bệnh sẽ sinh ra tổng số cá thể bệnh:

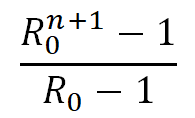
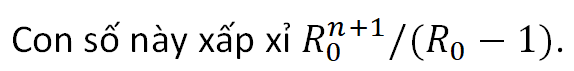
Ví dụ 1: Các chủng COVID-19 có các trung bình của khoảng thời gian nối tiếp gần như nhau và loanh quanh 4, nên ta giả sử T = 4 ^[1,2]. Với 20 ngày, ta có n = 20 / T = 20 / 4 = 5.

Bảng dưới cho tổng số ca sau 20 ngày với các giá trị khác nhau của R₀ ^[3].

Ví dụ 2: R₀ lớn không nói lên được vấn đề nếu thiếu T. Cặp (R₀ = 5, T = 4) sẽ khiến số ca tăng nhanh hơn cặp (R₀ = 25, T = 8) cho dù 25 lớn hơn 5 nhiều.

Với R₀ lớn và T nhỏ, số ca tăng lên rất nhanh nên ta phải phong tỏa chặt hơn khi quá khả năng truy vết.

2. Phát hiện một ổ dịch

Giả sử ta không có điều kiện xét nghiệm tầm soát toàn dân, vậy làm thế nào để phát hiện một ổ dịch và số ca trong ổ dịch là bao nhiêu khi ta phát hiện ra?

Để giải quyết bài toán này, ta cần thêm hai tham số ngoài R₀ và T. Gọi p là xác suất một người sẽ đến viện do mắc bệnh. Gọi t là số ngày trung bình từ khi mắc bệnh cho tới khi đi bệnh viện. Với COVID-19, số ca có triệu chứng chiếm ít nhất 20% và số ca nặng ít nhất là 3% nên ta tạm giả thiết p = 10%. Những ai mắc COVID-19 và có triệu chứng, thì trung bình triệu chứng xuất hiện sau 5 ngày mắc nên ta giả thiết t = 7.

Trước tiên ta tính số ca tối thiểu để phát hiện ra ổ. Giả sử ta phát hiện ra ổ khi có người mắc đi viện. Xác suất để ổ dịch có m người mà vẫn chưa ai đi viện là (1 - p)^m (nên ta chưa phát hiện ra ổ). Vậy ta cần m = 29 thì xác suất này mới là 0.9²⁹ = 4.7% < 5%. Tức là ta phát hiện ra ổ với xác suất 95% khi ổ có đến 29 ca.

Tiếp theo ta quy đổi số ca tối thiểu ra số ngày. Giả sử T = 4, bảng dưới cho kết quả với các giá trị khác nhau của R₀.

Với R₀ lớn, số ca khi ta phát hiện ra ổ rất lớn. Đặc biệt tốc độ số ca tăng rất nhanh như đã thấy trong mục trước, nên ta phải xem xét phong tỏa nhanh khi quá khả năng truy vết. Các ước lượng sẽ chính xác hơn nếu ta ước lượng được p và t thay vì tạm giả thiết. Phương pháp này không yêu cầu giá trị p quá chính xác. Ví dụng với chủng Delta, p từ 10% đến 20% cho kết quả như nhau. Tuy nhiên nếu p = 5% (như có triệu chứng mà không đi viện, hoặc đi viện mà không hẳn đã được phát hiện ra) và t = 10 thì sẽ là tai họa với chủng Delta (tổng số ca khi phát hiện ổ lên tới khoảng 2600).

Cuối cùng ta chú ý rằng tổng số ca khi phát hiện ổ chỉ là tổng số ca hôm nay, nên số ca tương lai tiếp tục tăng. Kể cả ta áp các biện pháp phong tỏa và hệ số lây nhiễm giảm xuống 1, thì cứ 4 ngày, tổng số ca trong 4 ngày cuối cùng (chứ không phải toàn bộ 781 ca trong trường hợp Delta) lại lây ra chừng đó ca nữa. Phần tiếp theo và bài về dự báo sẽ nói sâu thêm về điều này.

3. Đánh giá diễn biến dịch qua số ca mới mắc mỗi ngày

Ở phần trên ta đánh giá nguy cơ khi dịch mới bắt đầu. Điều này là khả thi khi một chủng virus xuất hiện ở nước ta sau khi đã xuất hiện vài tháng ở nước khác. Lúc đó các tham số đã được ước lượng trước.

Khi bệnh dịch diễn ra, số người có miễn dịch do đã mắc bệnh hoặc được tiêm vắc-xin tăng lên, và ta cũng thay đổi liên tục các biện pháp chống dịch. Khi đó để đánh giá dịch, ta không sử dụng R₀ mà sử dụng một hệ số tổng quát hơn R₀. Đó là hệ số lây nhiễm thực R_e (effective reproduction number).

Gọi V_t là số ca mới mắc bệnh ngày thứ t. Giả sử T = 4, khi đó R_e tại thời điểm t được ước lượng bởi tổng số ca T ngày tương lai chia cho tổng số ca T ngày gần nhất (khi mẫu số dương),

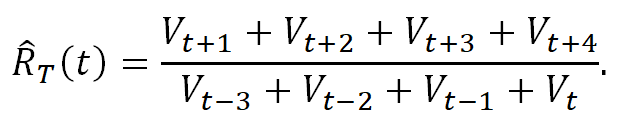
Trong giai đoạn đầu của dịch, ta có bảng đánh giá sau.

Tương tự như GDP trong kinh tế, R_T có thể được tính cho từng vùng, tỉnh, hay thành phố và nó bị ảnh hưởng bởi rất nhiều yếu tố như khẩu trang, vệ sinh, mật độ dân số, quãng đường đi trung bình, cách ly, giãn cách .v.v. Do đó ta cần thêm các phân tích khác để hiểu yếu tố nào tác động đến sự biến đổi của R_T.

4. Áp dụng cho đợt dịch từ cuối tháng 4/2021

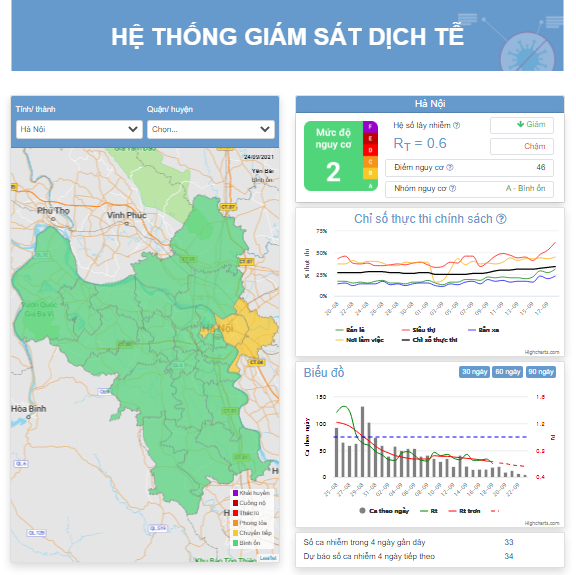
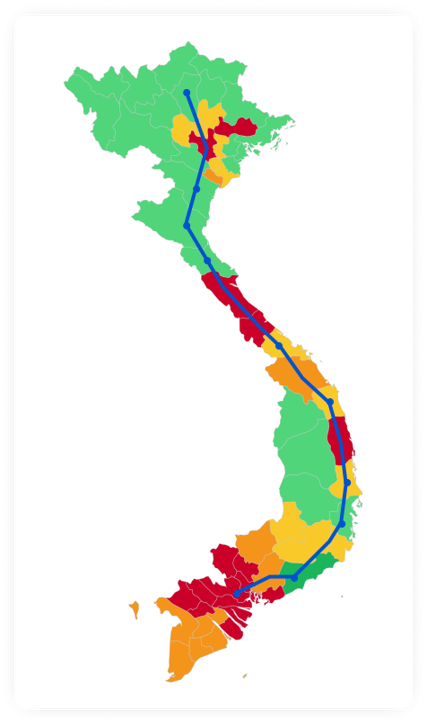
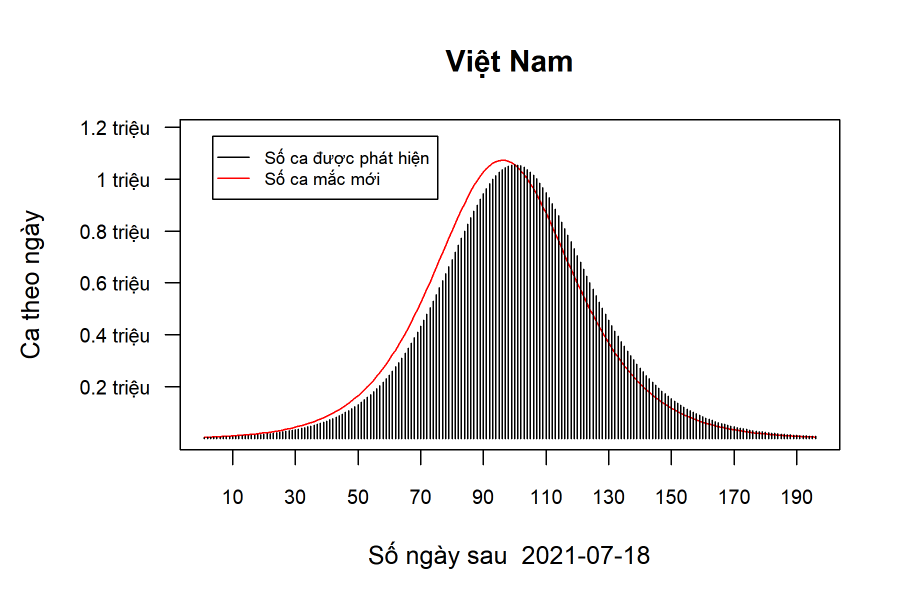
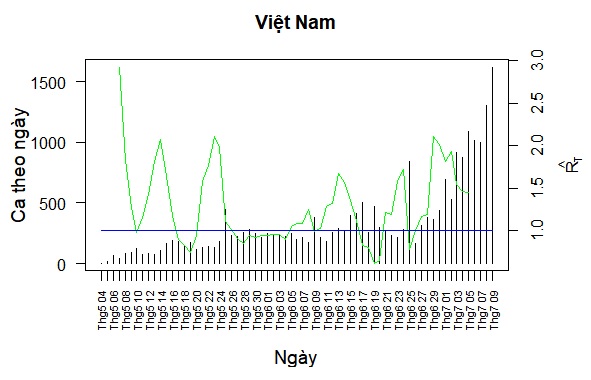
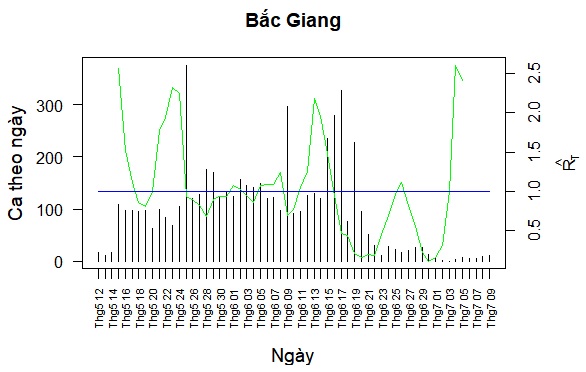
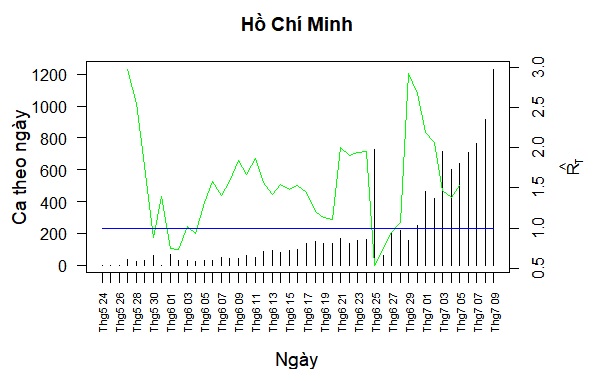
Ta tính R_T cho đợt dịch COVID-19 ở Việt Nam (VN) bắt đầu vào cuối tháng 4/2021. Dữ liệu số ca mắc mới mỗi ngày trên Việt Nam và tại mỗi tỉnh/thành phố được lấy từ VnExpress ^[4]. Ta loại bỏ khoảng 4 đến 7 giá trị ban đầu của R_T do dữ liệu không ổn định trong các ngày đầu mới phát hiện ổ dịch. Chúng tôi tạm thời chỉ tính R_T cho Việt Nam và hai tỉnh/thành phố có số ca nhiều nhất, Bắc Giang (BG) và Hồ Chí Minh (HCM). Khi tính R_T cho một tỉnh, ta bỏ qua sai số tạo bởi các ca dịch chuyển giữa các tỉnh.

Ta nhận thấy ba đỉnh của R_T,VN vào các ngày 14/5, 22/5, và 13/6 tương ứng với ba đỉnh của R_T,BG. Hai đỉnh của R_T,VN vào các ngày 24/6 và 29/6 tương ứng với hai đỉnh của R_T,HCM. Đây là lý do ta cần phân tích riêng rẽ BG và HCM.

Đối với BG, do năng lực xét nghiệp ban đầu không bằng năng lực cách ly, nên R_T,BG biến đổi mạnh. Tuy nhiên R_T,BG > 1 chỉ diễn ra trong các khoảng thời gian trên dưới 1 tuần, và đặc biệt có giai đoạn dài loanh quanh 1. Điều này cho thấy BG kiểm soát tốt.

Đối với HCM, R_T,HCM loanh quanh 1.5 nên số ca tăng dần. R_T,HCM có giảm trong khoảng 4 ngày từ 17/6 đến 20/6 (nhưng vẫn trên 1), tuy nhiên khoảng thời gian này quá ngắn nên không phải là xu hướng. Sau khi phát hiện thêm ổ dịch thì R_T,HCM lập tức tăng lại. R_T,HCM sau đó giảm xuống dưới 1 trong 4 ngày, nhưng đây là do số ca phát hiện bị cộng dồn chứ không phải do kiểm soát dịch tốt (quãng thời gian 4 ngày là ngắn không thể hiện xu hướng). Điểm khác biệt lớn nhất giữa BG và HCM là HCM không có giai đoạn dài nào mà thực sự R_T,HCM loanh quanh 1 hay có xu hướng giảm mạnh để cho thấy việc kiểm soát dịch là hiệu quả.

Đối với chủng Delta, như đã phân tích ở trên, khi một ổ dịch mới được phát hiện qua người bệnh đến viện thay vì xét nghiệm tầm soát thì số ca trong ổ có thể tương đối lớn. Do đó nếu ta không kiểm soát tốt R_T thì nên tính toán các biện pháp phong tỏa mới mạnh hơn và nhanh hơn (so với khi dập các chủng COVID-19 trước).

5. Xét nghiệm gộp

Để giảm chi phí xét nghiệm, ta gộp nhiều mẫu xét nghiệm chung. Thuật toán là ta xét nghiệm gộp g mẫu, nếu âm tính thì toàn bộ các mẫu trong đó là âm tính, nếu dương tính thì ta xét nghiệm riêng từng mẫu trong đó. Có nghiên cứu chỉ ra rằng ta có thể gộp đến 64 mẫu ^[5]. Câu hỏi đặt ra là đâu là giá trị tối ưu cho g?

Chúng tôi chưa có thời gian để cho một câu trả lời thỏa đáng, nên chúng tôi chỉ có vài ý kiến tạm thời. Gọi tổng số dân là N và tỷ lệ số ca bệnh trong toàn dân là q. Ví dụ N = 200 và chỉ 1 ca bệnh trong đó (q = 1/200), ta có bảng sau.

Ta thấy rằng không phải cứ gộp càng nhiều là càng tốt. Giá trị tối ưu của g phụ thuộc q. q càng nhỏ thì giá trị tối ưu của g càng lớn (tỷ lệ ca bệnh càng nhỏ thì ta càng có thể gộp nhiều mẫu).

Nhận xét tiếp theo là trường hợp xấu nhất xảy ra khi mỗi mẫu gộp chỉ có một ca bệnh, vì khi đó số mẫu ta phải xét nghiệm riêng lẻ là lớn nhất. Khi xét trường hợp xấu nhất, ta có thể quy bài toán trên về bài toán đơn giản hơn như trong ví dụ trên. Khi đó tổng số dân là 1/q và chỉ có 1 ca bệnh.

Để giải bài toán tổng quát, chúng tôi nghĩ rằng ta có thể sử dụng phương pháp mô phỏng.

6. Phần kết

Ở trên chúng tôi đã trình bày cụ thể cách đánh giá nguy cơ khi dịch mới bắt đầu và cách đánh giá diễn biến dịch. Để biết thêm chi tiết, các bạn có thể xem thêm hai slide đính kèm. Các bạn có thể tìm đọc cách ước lượng T và R₀ trong các tài liệu tham khảo dưới đây. Chúng tôi áp dụng các phương pháp này với đợt dịch COVID-19 mới nhất ở Việt Nam. Chúng tôi cũng trình bày qua về số mẫu gộp tối ưu trong xét nghiệm. Chúng tôi sẽ bàn thêm về các chủ đề khác như dự báo, các phương pháp xét nghiệm, xác suất dương/âm tính giả, vắc-xin .v.v. trong các bài viết sau.

- trunght@onyx.vn -

Tài liệu tham khảo

(Xem thêm 11 tài liệu tham khảo khác trong 2 slide đính kèm)

SIR (thời gian rời rạc và tham số thay đổi): SIR review - 210709.pdf

Đánh giá diễn biến dịch qua số ca mới mắc mỗi ngày: time-since-infection model - 210710.pdf

1. Geismar, C. et al. Serial interval of COVID-19 and the effect of Variant B.1.1.7: analyses from a prospective community cohort study (Virus Watch). medRxiv 2021.05.17.21257223 (2021). doi:10.1101/2021.05.17.21257223

2. Pung, R., Mak, T. M., group, C. C.-19 working, Kucharski, A. J. & Lee, V. J. Serial intervals observed in SARS-CoV-2 B.1.617.2 variant cases. medRxiv 2021.06.04.21258205 (2021). doi:10.1101/2021.06.04.21258205

3. Wikipedia. Variants of SARS-CoV-2. Available at: https://en.wikipedia.org/wiki/Variants_of_SARS-CoV-2.

4. Số liệu Covid-19 tại Việt Nam. Available at: https://vnexpress.net/covid-19/covid-19-viet-nam. (Accessed: 10th July 2021)

5. Yelin, I. et al. Evaluation of COVID-19 RT-qPCR test in multi-sample pools. medRxiv 2020.03.26.20039438 (2020). doi:10.1101/2020.03.26.20039438

Bình luận:

Chưa có bình luận nào.

Thông tin bình luận:

Chưa nhập họ tên.

Chưa nhập email.

Gửi